You can submit your questions regarding Theano, Blocks and Fuel, and the class project, as well as general revision questions in the lead-up to the exam, on this page.
Similarly to the Q&A style in the rest of the course, please help out your fellow students if you know the answer to their questions.
When I am trying to follow this instruction, installing the data set, I do not know what do you mean “in order for Fuel to know where to look for its data, the data_path configuration variable has to be set inside ~/.fuelrc. It’s expected to be a sequence of paths separated by an OS-specific delimiter (: for Linux and OSX, ; for Windows):
# ~/.fuelrc
data_path: “/first/path/to/my/data:/second/path/to/my/data”
”
should i create a file called .fuelrc and have this content on that file?
LikeLike
I am sorry I forgot put the link:http://fuel.readthedocs.org/en/latest/built_in_datasets.html
LikeLike
The link:http://fuel.readthedocs.org/en/latest/built_in_datasets.html
LikeLike
Then I followed this :”cd $HOME
mkdir fuel_data # Create a directory in which Fuel can store its data
echo “data_path: \”$HOME/fuel_data\”” > ~/.fuelrc # Create the Fuel configuration file
cd fuel_data # Go to the data directory” I do not why i can not use fuel-download command. It seems that I did not install fuel successfully, is there a way to uninstall fuel?
LikeLike
In you have install fuel with pip, you have the bin file in ~/.local/bin/. So you can add this folder to your path or run fuel download with ~/.local/bin/fuel-download.
It’s not mandatory to have a .fuelrc, if you haven’t one, fuel-download will simply download the files in the current folder.
LikeLike
Just to clarify: The Fuel scripts are only in
~/.local/binif you’re not using Anaconda; otherwise the file is most likely in~/anaconda2/binor~/anaconda3/bin.Secondly,
fuel-downloadwill always download the file to the current working directory. Likewise,fuel-convertwill read and write files to the current working directory by default. The data path in~/.fuelrcis used is when you load the dataset in Python (e.g.train = DogsVsCats(('train',))), so you still need to set it.LikeLike
Thanks for the explanation, I have a question about the hd5 file. I am using fuel-convert and after 40% I got a file of 4.3Gb So, I suppose the final file will be bigger than 10Gb, is it normal ? Isn’t it a way to reduce that file ? (Maybe using another datatype for the numpy array ?)
LikeLike
Yes, the final file is about 16GB. There’s no easy way to reduce that file size, the images are already stored using unsigned 8-bit integers, which is the smallest data type possible. The reason it’s so big compared to the original files is that the data is stored without compression, while the original files were JPEG files. (You could store the data in JPEG, but you would have to decompress each batch of images during training, which could be slow.) If you don’t have 16GB of memory, don’t worry. HDF5 is pretty good at reading things from disk for large files and caching intelligently.
LikeLiked by 1 person
I do not why I get this error when I use fuel-download
home/2014/dchen53/fuel_data/dogs_vs_cats.train.zip: 99% [] ETA: 0:00:01 2.3/home/2014/dchen53/fuel_data/dogs_vs_cats.train.zip: 99% [] ETA: 0:00:00 2.3 MiB/s
Traceback (most recent call last):
File “/home/2014/dchen53/anaconda2/bin/fuel-download”, line 9, in
load_entry_point(‘fuel==0.1.1’, ‘console_scripts’, ‘fuel-download’)()
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/fuel/bin/fuel_download.py”, line 62, in main
download_function(**args_dict)
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/fuel/downloaders/base.py”, line 142, in default_downloader
download(url, file_handle)
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/fuel/downloaders/base.py”, line 68, in download
r = requests.get(url, stream=True)
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/requests/api.py”, line 69, in get
return request(‘get’, url, params=params, **kwargs)
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/requests/api.py”, line 50, in request
response = session.request(method=method, url=url, **kwargs)
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/requests/sessions.py”, line 468, in request
resp = self.send(prep, **send_kwargs)
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/requests/sessions.py”, line 597, in send
history = [resp for resp in gen] if allow_redirects else []
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/requests/sessions.py”, line 195, in resolve_redirects
**adapter_kwargs
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/requests/sessions.py”, line 576, in send
r = adapter.send(request, **kwargs)
File “/home/2014/dchen53/anaconda2/lib/python2.7/site-packages/requests/adapters.py”, line 433, in send
raise SSLError(e, request=request)
requests.exceptions.SSLError: EOF occurred in violation of protocol (_ssl.c:590)
LikeLike
There seems to be a problem with your SSL configuration. Did you try updating or reinstalling
opensslusing e.g.conda update opensslorconda install -f openssl?LikeLiked by 1 person
Thanks, my computer runs out of memory, and with the new server you give me, I do not have the issue
LikeLike
https://obilaniu6266h16.wordpress.com/2016/02/04/einstein-summation-in-numpy/
I don’t know if he’s posted it somewhere, but Olexa’s post on numpy’s einsum is excellent. Einsum is a really general way to do linear algebra things, where you only have to think about the dimensions of the matrices you have, and specify that in a string.
Not sure if this picture will show up, but it shows how it allows you to implement forward prop and backprop in less than a dozen lines.
LikeLike
I do not know why I get this error when i am doing the blocks tutorial
LikeLike
I fixed my problem by updating theano to developer version
LikeLike
On Hades, I encountered this message after trying to use GPUs with theano :
WARNING (theano.tensor.blas): Failed to import scipy.linalg.blas, and Theano flag blas.ldflags is empty. Falling back on slower implementations for dot(matrix, vector), dot(vector, matrix) and dot(vector, vector) (libquadmath.so.0: cannot open shared object file: No such file or directory)
I didn’t do anything to THEANO’s setting and ran the code after import the module using “module add theano” on the cluster.
LikeLike
I have published a post about how to use the cluster:
https://florianbordes.wordpress.com/2016/02/09/how-to-use-the-cluster-of-calcul-quebec/
Don’t try to use the modules (The versions available doesn’t match with what we need) and install anaconda directly.
LikeLike
Hello, Bart, you sent us an email about moving our dog_cats dataset to common folder, I followed this instruction: But get this error:
I do not know why:
from fuel.datasets.dogs_vs_cats import DogsVsCats
Traceback (most recent call last):
File “”, line 1, in
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/fuel/init.py”, line 2, in
from fuel.config_parser import config # noqa
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/fuel/config_parser.py”, line 209, in
config.load_yaml()
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/fuel/config_parser.py”, line 129, in load_yaml
for key, value in yaml.safe_load(f).items():
AttributeError: ‘str’ object has no attribute ‘items’
Here is my .fuelrc content: data_path:”/home2/ift6ed05/fuel_data”:”/home2/COMMON”
Here is my .bashrc content:
export PATH=”/home2/ift6ed05/anaconda2/bin:$PATH”
export PATH=”$PATH:$HOME/ffmpeg-2.8.6/bin”
export FUEL_DATA_PATH=/home/COMMON:$HOME/fuel_data
And I did source .bashrc after adding this line.
LikeLike
And if I run this command,
I get similar error:
fuel-download dogs_vs_cats
Traceback (most recent call last):
File “/home2/ift6ed05/anaconda2/bin/fuel-download”, line 9, in
load_entry_point(‘fuel==0.1.1’, ‘console_scripts’, ‘fuel-download’)()
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/setuptools-19.6.2-py2.7.egg/pkg_resources/init.py”, line 547, in load_entry_point
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/setuptools-19.6.2-py2.7.egg/pkg_resources/init.py”, line 2719, in load_entry_point
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/setuptools-19.6.2-py2.7.egg/pkg_resources/init.py”, line 2379, in load
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/setuptools-19.6.2-py2.7.egg/pkg_resources/init.py”, line 2385, in resolve
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/fuel/init.py”, line 2, in
from fuel.config_parser import config # noqa
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/fuel/config_parser.py”, line 209, in
config.load_yaml()
File “/home2/ift6ed05/anaconda2/lib/python2.7/site-packages/fuel/config_parser.py”, line 129, in load_yaml
for key, value in yaml.safe_load(f).items():
AttributeError: ‘str’ object has no attribute ‘items’
LikeLike
I think it’s :
export FUEL_DATA_PATH=/home2/COMMON
instead of /home/COMMON, the repository /home/COMMON doesn’t exist.
Or if you want to use the fuelrc file, it’s:
data_path: “/home2/COMMON:/home2/ift6ed05/fuel_data”
LikeLike
After I changed to home2, I have the same error.
LikeLike
I missed this comment earlier, but in case you still have the same error: It seems to say there is something wrong with your
.fuelrcfile. It should contain something likedata_path: /home2/COMMONbut instead it seems to contain just a string.LikeLike
Hello, Bart, it still has the same problem, I reinstalled ananconda, fuel, blocks, it has solved the problem , but sadly I am downloading the fuel data on my home folder. Wishing it does not give much trouble.
LikeLike
Just wondering if there is a technique which can resume from one program when my computer is suddenly shut down.
LikeLike
Instead of rerunning one program from start
LikeLike
This is called checkpointing, and there are many different ways it can be achieved at varying degrees. With neural network training, you generally just want to make sure that you store your parameters every N steps, so that you can resume training from those parameters when things go wrong. Blocks implements this using the
Checkpointextension, which will allow you to resume training easily.LikeLike
I encountered this problem when trying to get data from a server stream.
In one notebook I set up a minimalistic server as follows:
<br />from fuel.datasets.dogs_vs_cats import DogsVsCats from fuel.streams import DataStream from fuel.schemes import ShuffledScheme train = DogsVsCats(('train',), subset=slice(0, 20000)) stream = DataStream(train, iteration_scheme=ShuffledScheme(train.num_examples, 128)) from fuel.server import start_server start_server(stream)Then in another notebook I initiate an instance of Serverstream and try to get one batch from the server as follows:
<br />from fuel.streams import ServerDataStream data_stream = ServerDataStream(('image_features','target'),False) iterator = data_stream.get_epoch_iterator() one_batch = next(iterator)which then returns this error :
<br />--------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-6-82a2181a96af> in <module>() 2 data_stream = ServerDataStream(('image_features','target'),False) 3 iterator = data_stream.get_epoch_iterator() ----> 4 one_batch = next(iterator) /Users/patricklau/anaconda3/lib/python3.5/site-packages/fuel/iterator.py in __next__(self) 30 data = self.data_stream.get_data(next(self.request_iterator)) 31 else: ---> 32 data = self.data_stream.get_data() 33 if self.as_dict: 34 return dict(zip(self.data_stream.sources, data)) /Users/patricklau/anaconda3/lib/python3.5/site-packages/fuel/streams.py in get_data(self, request) 231 if not self.connected: 232 self.connect() --> 233 data = recv_arrays(self.socket) 234 return tuple(data) 235 /Users/patricklau/anaconda3/lib/python3.5/site-packages/fuel/server.py in recv_arrays(socket) 73 data = socket.recv() 74 buf = buffer_(data) ---> 75 array = numpy.frombuffer(buf, dtype=numpy.dtype(header['descr'])) 76 array.shape = header['shape'] 77 if header['fortran_order']: ValueError: cannot create an OBJECT array from memory bufferLikeLike
Judging from the error, you are trying to use the server to send object arrays i.e. NumPy arrays that contain Python objects instead of sending an n-dimensional tensor.
You will need to crop the images to be of the same size, so that you can send a single NumPy array with the shape
(batch, channel, height, width)instead of sending a list of arrays whereheightandwidthare different, which is what you’re currently trying to do.LikeLike
How do you preview a reply comment before posting it?
LikeLike
Interesting question!
I do the stupid hack of posting the comment on my blog and then deleting it 🙂
I hear there are comment preview plugins…
https://lorelle.wordpress.com/2006/04/01/comment-live-preview-placement/
LikeLike
Just wondering should we use the test set to do predictions, as we have no labeled data for the test set, how do we know the accuracy?
LikeLike
Is anyone training a feed-forward neural network with Batch Normalization? If so, what are your strategies to learn the validation-time mean and variance: Compute over full training set, or a random subset?
Also, is anyone training a neural network with many BN layers? If so, how do you efficiently manufacture all of the “partial” neural networks (Input-to-BN1, Input-to-BN2, Input-to-BN3, …) and efficiently learn the validation-time mean and variance for each BN layer one after the other? Or are there other strategies to bypass this annoyance?
LikeLike
Pingback: Questions | IFT6266 H-2016 Deep Learning
I have a qustion about mini batch training, if my training set is smaller than my validation set ,like training set is 5000, validation set is 45000, should I do mini batch on the validation set too, otherwise I am facing memory issue.
LikeLike
I don’t want to put the question on one of the lectures from way back, so I will put it here.
This question is about the initialization methodology proposed by Glorot and Bengio (2010) and its application in the context of convolutional networks.
In the paper, it was suggested to initialize each layer of an mlp with sqrt(6)/(sqrt(n_i + n_(i+1)), where n_i is the number of units in the current layer and n_(i+1) the number of units in the next layer.
How would we adapt it to conv nets ? In one of the deep learning tutorials with theano the initialization was implemented as
n_i = num input feature maps * filter height * filter width
n_(i+1) = num output feature maps * filter height * filter width / pooling_size
Can someone explain where these numbers come from? It is not immediately obvious how to interpret a convolutional layer as an mlp layer in order to understand the initialization. First there is the issue of number of dimensions, then it is that of converting a conv net to a mlp .
LikeLiked by 1 person
This confused me too, but I think I found clarity by looking at Caffe’s source code.
This blog post (http://andyljones.tumblr.com/post/110998971763/an-explanation-of-xavier-initialization) talks about Xavier/Glorot initialization, and links to Caffe’s implementation here (https://github.com/BVLC/caffe/blob/737ea5e936821b5c69f9c3952d72693ae5843370/include/caffe/filler.hpp#L129-143)
Therein, we learn from the comments at lines 137-140 that:
It fills the incoming matrix by randomly sampling uniform data from [-scale, scale] where scale = sqrt(3 / fan_in) where fan_in is the number of input nodes. You should make sure the input blob has shape (num, a, b, c) where a x b x c = fan_in.
LikeLike
I don’t see how he makes it any clearer about the application in conv nets. In a convolutional network, what we think of as one sample (an image) is not one sample when the conv net is thought of as an mlp, otherwise we would take
n_in = num input feature maps * num image row * num image column
If we think of an image as many samples, each of which a local window the size of the filter (3 x 3, say), then we still leave
n_out = num output feature maps * num filter row * num filter column / pool size
unexplained. The formula above is essentially saying that we are looking at the convolution operation as mapping from R^(n_in) to R^(n_out), only that is not true.
Take a simple example where the incoming feature maps are just the three channels of the original image. Assume there are only two output feature maps and we focus on W_1, a 2 x 2 filter that maps to the first output feature map.
n_in = num input feature maps * num image row * num image column
tells us that we are grouping the three 2×2 windows from the input channels as one sample and this gets mapped to 1 pixel in the output feature map.
I just don’t see how we could explain n_out.
LikeLike
The formulas you give identify:
1. The total number of inputs that contribute to any single output; This is called the fan-in.
2. The total number of outputs to which any single input contributed; This is called the fan-out.
Visualize a tensor of size
(#InputMaps, Height, Width)with all elements = +1.0, as if generated bynumpy.ones(). Also visualize a convolution filter of size(#OutputMaps, #InputMaps, FHeight, FWidth), whose every filter tap is also = +1.0.If you perform the convolution, you will find that the output tensor is not an array of +1.0’s of size approximately
(#OutputMaps, Height, Width). Instead, every entry will be equal to#InputMaps * FHeight * FWidth. Because every filter-tap-by-image-pixel product is +1.0*+1.0 = +1.0, that proves that a large number of pixels contributed to this output. This number is called the fan-in, and that’s why fan-in is calculated as part of the computation of the normalization constant.A similar logic applies to the reverse direction in which gradients flow. We’re now interested in fan-out instead of fan-in, and there’s the additional complexity of pooling, which cuts down the effective number of outputs to which a single output is connected (the definition of fan-out).
The square roots in the formulas relates to the behaviour of a sum of independent variables. Going back to the convolution filter of size
(#OutputMaps, #InputMaps, FHeight, FWidth)above, imagine that instead of every filter tap and image pixel being = +1.0, you have 50% chance of being +1.0 and 50% chance of being -1.0. The variance of the sum of N independent random variables is the sum of the variances, so its standard deviation (the expected magnitude of the sum) will be the square root of that. The “gain” of the filter in the forward direction will thus be on the order of the square root of fan-in. The same sort of logic applies to the reverse direction and fan-out.Alternatively, you can view the computation of a filter’s output as having random walk behaviour (https://en.wikipedia.org/wiki/Random_walk). The filter-tap-by-image-pixel products from my example above are +1 or -1 with 50% probability each, and the sequential accumulation of partial products constitutes a random walk. Given that it’s a random walk, the expected distance from 0.0 (and thus, the magnitude of the activation) will be on the order of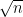 after
after  partial product accumulations. Therefore, after
partial product accumulations. Therefore, after
fan_inaccumulations, the filter’s expected “gain” is proportional tosqrt(fan_in), and the normalization constant is the inverse of that.sqrt(2.0/(fan_in + fan_out))is a compromise normalization constant between the forward and backwards directions.LikeLike
Another convolutional network related question: in most of the literature we follow a convolution operation by a non-linear activation function and then a downsample operation. However, in theano’s deep learning tutorial it is actually implemented as a convolution->downsample->tanh sequence. Does it make any difference whether we downsample or apply non-linear activation first ? In this case it seems like the theano tutorial implemented the conv layer incorrectly. But it begs the question of why the literature always construct a conv layer by stacking convolution->non-linear activation -> downsample sequences. Also, it doesn’t seem like there is theoretical justification to favour one way over the other, does it ?
LikeLike
If the pooling is a max-pooling layer and the non-linearity is monotonically increasing (ReLU, tanh, sigmoid and numerous others are), then the pooling and non-linearity layers can commute, because the locally maximal pre-activation before the non-linearity will correspond to a locally maximal activation after it.
So if either order is equivalent, the decision is purely computational. Doing a (2,2) max-pooling and then applying a monotonically-increasing non-linearity costs (2*2) = 4x less in non-linearity evaluations than doing the reverse, yet they produce bitwise-identical results.
The bad news: This doesn’t apply to avg-pooling. The good news: I can’t think of a single non-monotonically-increasing non-linearity in use.
LikeLike
I am wondering if we could use pertained network like VGG NET something like that to train our model?
LikeLike
April Fools joke from Kaggle I believe:
LikeLiked by 2 people
In class, I had proposed for the Voice Synthesis project that instead of directly generating the waveform, and thus having to deal with continuity issues, that one could try modulating a bank of sinusoids. Yoshua grokked what I had suggested and wrote it down on the board, but afterwards I came up with an improvement. If we always require two signals of each frequency, one phase-offset by 90 degrees from the other, then by an appropriate choice of amplitudes of each one may always synthesize an arbitrary phase shift, without an explicit phase parameter. I summarize this in my blog post here:
https://obilaniu6266h16.wordpress.com/2016/04/07/idea-for-continuous-voice-modulation-in-the-voice-synthesis-project/
LikeLike
I am wondering if anyone knows how to deal with dark spots when you rotate your image, i know cropping is one way.Here is one example i rotate:http://s8.postimg.org/917d27ztd/rotate_8_dog_9452.jpg
LikeLiked by 1 person
Part of the reason why I constructed my dataset with inpainted 256×256 images, yet use a 192×192 input, is to allow some wiggle room to rotate and translate without black patches appearing.
But on the other hand, an argument can be made that these black patches should stay, because your neural network should learn to be robust to junk at the very border. It might be useful to fill that black area with random noise for that very reason.
LikeLike
Why is L2 Regularization equivalent to a Gaussian prior?
LikeLike
Why is L2 Regularization equivalent to a Gaussian prior?
LikeLike
Let’s try an answer.
I’m gonna start by the definition of the L2 regularization given in the book (p231).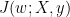 an other cost function which is :
an other cost function which is : 
The L2 regularization means to use instead of
Now let’s see what means taken a Gaussian prior over the parameters when you update them:

You have done your training on the input X , and you want to find better parameters w knowing those inputs, If you do a MAP :
You want to maximize over w:
Which is the same to maximize over w: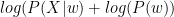
At this point if you do an identification : is homogeneous to the probability of the inputs given the parameters so it’s homogeneous to the cost function
is homogeneous to the probability of the inputs given the parameters so it’s homogeneous to the cost function 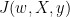
–
If you have a prior Gaussian over w, for example:
(you throw away the constant because it doesn’t change anything when you maximize the formula and will be vanish if you derive)
So by using an L2 regularization, we act like you perform a MAP with the Gaussian prior over your weight and you maximize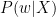 by doing your gradient descent.
by doing your gradient descent.
LikeLiked by 1 person
Please demonstrate
LikeLike
Why is L1 Regularization equivalent to a Laplacian Prior?
LikeLike
Like for the previous answer :

L1 definition :
if
By doing an MAP on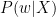

You use:
And you find the connection between the 2 interpretations.
LikeLiked by 1 person
I have gotten to the same points as you in the demonstration of L2 being equivalent to a Gaussian prior and L1 being equivalent to a Laplacian prior. The only point that I think is missing is how you get to:
1. $w^Tw \sim \mathbb{N}(\frac{I}{\alpha},0)$
2. $w \sim Laplace(0,\frac{1}{\alpha})$
You just needed to add that for L2:
P(w)=\frac {1}{\sqrt {2\pi}\sigma}e^{-\frac {(w-\mu)^2}{2\sigma^2}}\
logP(w) = c_{1}w^{2} if\ \mu = 0\ which\ is\ the\ case\ when\ w \sim \mathbb{N}(\frac{I}{\alpha},0)
And for L1, it is probably some similar derivation but I don’t know the formula for the LaPlacian distribution
LikeLike
You can find the Laplace formula on :
https://fr.wikipedia.org/wiki/Loi_de_Laplace_%28probabilit%C3%A9s%29
You get the distribution (Gaussian or Laplacian) by choosing it. You make the assertion that the distribution of your weight is Gaussian (or Laplacian), this is a knowledge a priori you want to include in your network. (Does it answer your question?)
LikeLike
Welll I answered the missing link to go from Normal prior to W^2 above. That was all. Thanks
LikeLike
What is the conditional log-likelihood interpretation of the squared error
loss ?
LikeLike
You can look at linear regression in a probabilistic fashion, in which the likelihood, , is a Gaussian density that is
, is a Gaussian density that is  , where
, where 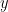 is the mean and
is the mean and  is the variance. If you take the log of the density, then you can get rid of the normalising constant (and the sigma term), in which you get the typical squared error term
is the variance. If you take the log of the density, then you can get rid of the normalising constant (and the sigma term), in which you get the typical squared error term  .
.
LikeLike
For a neural network, what loss function that makes sense for binary targets can be
interpreted as a minus a conditional log-likelihood ?
LikeLike
Isn’t it Cross-Entropy?
LikeLike
Yes. Can anyone prove it?
LikeLike
For derivation, check out slide 12:
Click to access 06_binarychoice_2pp.pdf
The last line of the derivation is equivalent to the cross entropy for binary targets.
LikeLiked by 1 person
Consider a function f returning a random output given an input state x ∈ X ,
returning a new state x 0 ∈ X , i.e., f outputs a sample from a conditional distribution
Q(x0|x), and its successive application would generate a Monte-Carlo Markov chain.
Let P represent the asymptotic distribution of that chain (and assume it exists), i.e., a
distribution on the space X . What relationship must hold between P and Q?
LikeLiked by 1 person
The multiple application of Q to generate sample should make converge the set of sample into a set of sample representative of the P distribution, I think.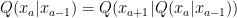 then Q=P
then Q=P
Or if
LikeLike
What is the difference between Sparse coding and Sparse autoencoders?
LikeLiked by 1 person
For the 2012 final, question 4: I’m not entirely sure what it’s asking. Is 1) a sparse autoencoder, and 2) a sparse denoising autoencoder? Or is 2 just a denoising autoencoder? In either case, I don’t see how c) corruption level factors into 1 – doesn’t it become a denoising autoencoder as soon as you add noise to the input? Or are we also saying ithat you are adding noise to the target?
In general, for that question I’m not sure about the difference in behaviour between 1) and 2) (unless (c) doesn’t apply to (1) )
LikeLike